Finding dialect areas by means of bootstrap clustering
Wilbert Heeringa
Jain and Dubes (1988, p. 55) define cluster analysis as 'the process of classifying objects into subsets that have meaning in the context of a particular problem.' The goal of clustering is to identify the main groups in complex data. In dialectometry cluster analysis is a mean to find groups given a set of local dialects and their mutual linguistic distances. Goebl (1982) introduced cluster analysis in the field of dialectometry (see also Goebl 1984, 1993).
The weakness of cluster analysis is its instability; small differences in the distance matrix may strongly change the results (Jain et al. 1999, Nerbonne et al. 2008). Kleiweg et al. (2004) introduced composite cluster maps, which are obtained by collecting chances that pairs of neighbouring elements are part of different clusters as indicated by the darkness of the border that is drawn between those two locations. Noise is added to the clustering process which enables the authors to estimate about how fixed a border is. Nerbonne at al. 2008 use clustering with noise and bootstrap clustering to overcome instability.
Both the work of Kleiweg et al. (2004) and Nerbonne et al. (2008) focus on boundaries which may be weaker or stronger, i.e. they are gradual. This makes it harder to compare the maps with traditional dialect maps where the color distinctions give a visual representation of the borders between different dialect areas, for example, the map of Daan and Blok (1969).
We introduce a new flavour of bootstrap clustering which generates areas, similar to classical dialect maps. In our approach 1) we consider dialect groups as continua, i.e. each local dialect is not necessarily strongly related to any other local dialect in the same group; the local dialects in a group rather constitute a 'network' and 2) we take into account that not every local dialect can be classified with statistical confidence.
We perform a procedure consisting of four steps. First, we randomly select 1000 n items from n items with replacement. For each resampled set of items we calculate the aggregated distances. Second, on the basis of the distances we perform agglomerative hierarchical cluster analysis. We choose nearest neighbour clustering since we prefer this method reflecting the idea of dialect areas as continua. On the basis of the tree we determine the number of natural groups by means of the elbow method. Third, for each pair of dialects we count the number of times that both dialects are found in the same natural group. The number will vary between 0 (never) and 1000 (always). Fourth, when two dialects belong to the same group in more than 950 of the cases (95%), we mark them as 'connected.' In this way we will obtain networks which are the groups.
We apply the procedure to distances in the sound components measured with Levenhstein distance between a set of 86 Dutch dialects. We use material which was collected in the period 2008-2011. Recorded transcriptions of male speakers aged 60 years or older are used, 125 words per speaker.
Figure 1 shows the distances, a network map and an area map.
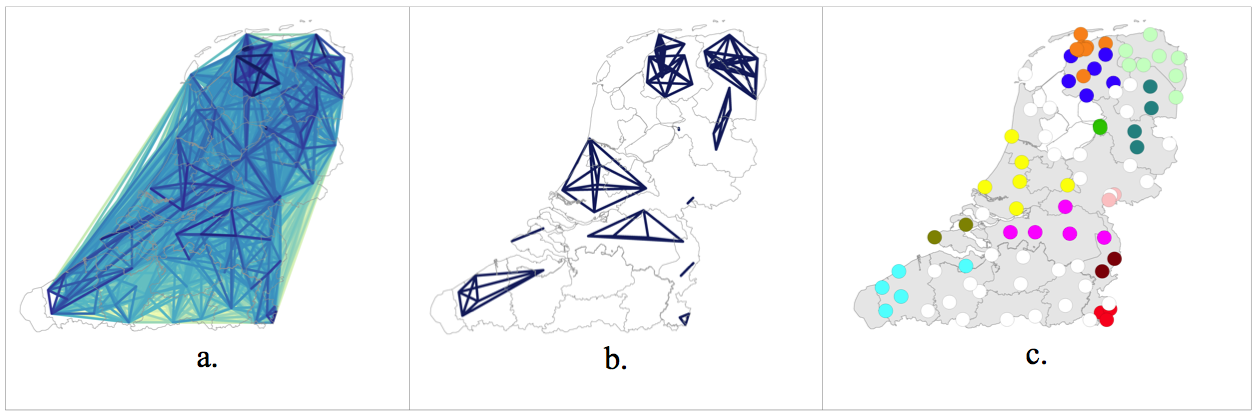
Figure 1. a) the distances: darker lines represent larger distances, b) network map, c) area map.
Literature
Daan, J. and Blok, D. P. (1969). Van Randstad tot Landrand; toelichting bij de kaart: Dialecten en Naamkunde. Bijdragen en mededelingen der Dialectencommissie van de Koninklijke Nederlandse Akademie van Wetenschappen te Amsterdam, volume XXXVII. Amsterdam: Noord-Hollandsche Uitgevers Maatschappij.
Goebl, Hans (1982). Dialektometrie. Prinzipien und Methoden des Einsatzes der Numerischen Taxonomie im Bereich der Dialektgeographie. Austrian Academy of Science, Wien.
Goebl, Hans (1984). Dialektometrische Studien: Anhand italoromanischer, rätoromanischer und galloromanischer Sprachmaterialien aus AIS und ALF, Vol. 3, Max Niemeyer, Tübingen.
Goebl, Hans (1993). Probleme und Methoden der Dialektometrie: Geolinguistik in globaler Perspektive. In: Viereck, W. (ed.), Proc. Internat. Congress of Dialectologists, Vol. 1. Franz Steiner Verlag, Stuttgart. 37-81.
Heeringa, Wilbert (2004). Measuring dialect pronunciation differences using Levenshtein distance. Groningen Dissertations in Linguistics 46. PhD thesis, University of Groningen.
Jain, A.K. and R. C. Dubes (1988). Algorithms for clustering data. Prentice-Hall, Inc. Upper Saddle River, NJ.
Jain, A. K., M.N. Murthy and P.J. Flynn, Data Clustering: A Review. ACM Computing Surveys, 31(3), 264-323.
Kleiweg, Peter, John Nerbonne and Leonie Bosveld (2004). Geographic Projection of Cluster Composites. In: Alan Blackwell, Kim Marriott and Atsushi Shimojima (eds.), Diagrammatic Representation and Inference. Third International Conference, Diagrams 2004. Cambridge, UK, March 2004 Lecture Notes in Artificial Intelligence 2980. Springer, Berlin. 2004. 392-394.
Nerbonne, John, Peter Kleiweg, Wilbert Heeringa and Franz Manni (2008). Projecting Dialect Differences to Geography: Bootstrap Clustering vs. Noisy Clustering. In: Christine Preisach, Lars Schmidt-Thieme, Hans Burkhardt, Reinhold Decker (eds.), Data Analysis, Machine Learning, and Applications. Proc. of the 31st Annual Meeting of the German Classification Society. Berlin: Springer. 647-654. (Studies in Classification, Data Analysis, and Knowledge Organization)
Last update: September 20, 2014. erik.tjong.kim.sang(at)meertens.knaw.nl